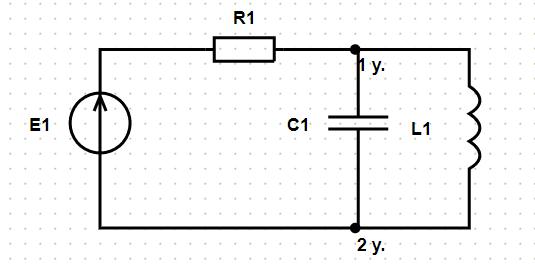
Нелинейные цепи постоянного тока. Графические методы расчета.
Расчеты разветвленных цепей можно вести, составляя уравнения по первому и второму законам Кирхгофа или методом контурных токов. Метод узловых потенциалов непосредственно непригоден. Объясняется это тем, что ток в любой ветви зависит не только от ЭДС находящегося в ней источника и от потенциалов тех узлов, к которым ветвь присоединена, но и от токов других ветвей, которые наводят ЭДС взаимной индукции.
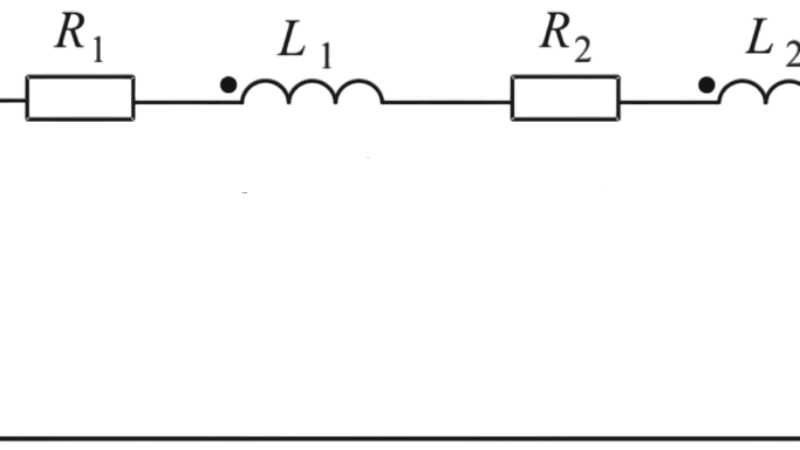
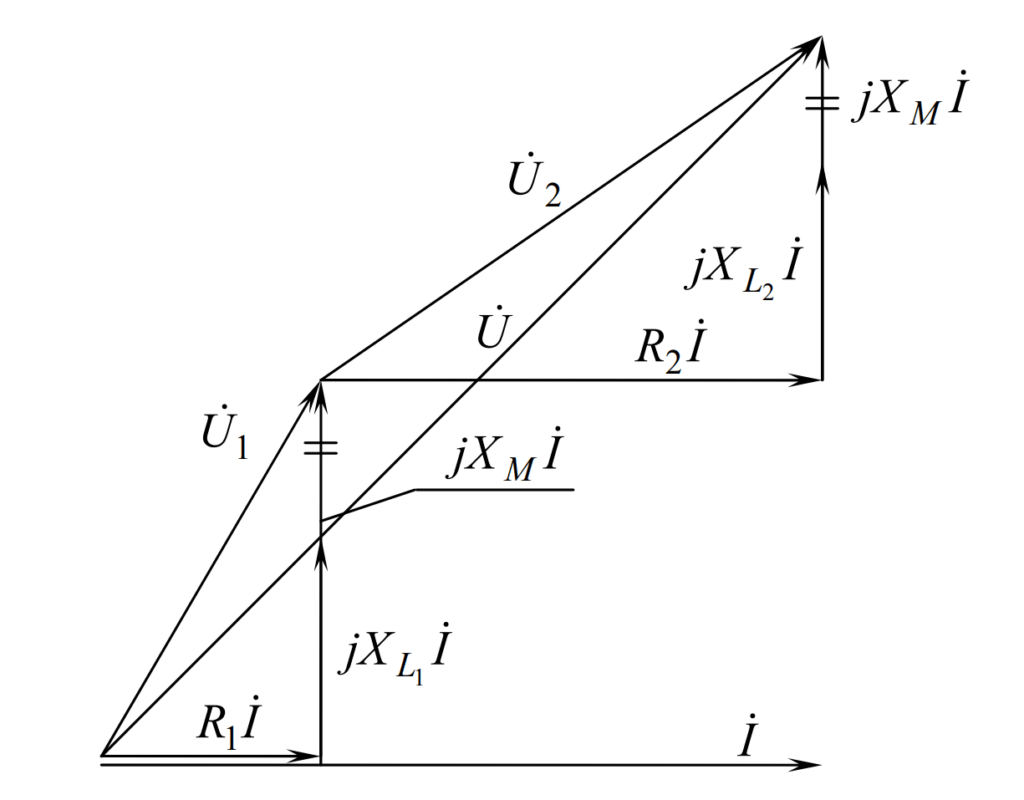

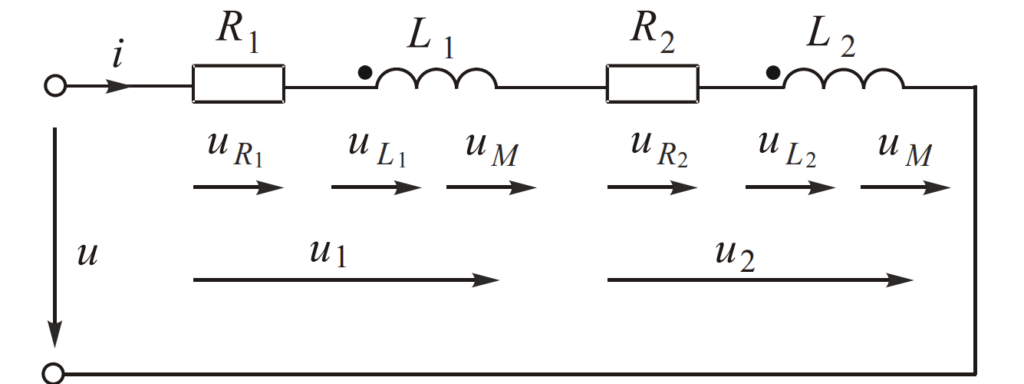
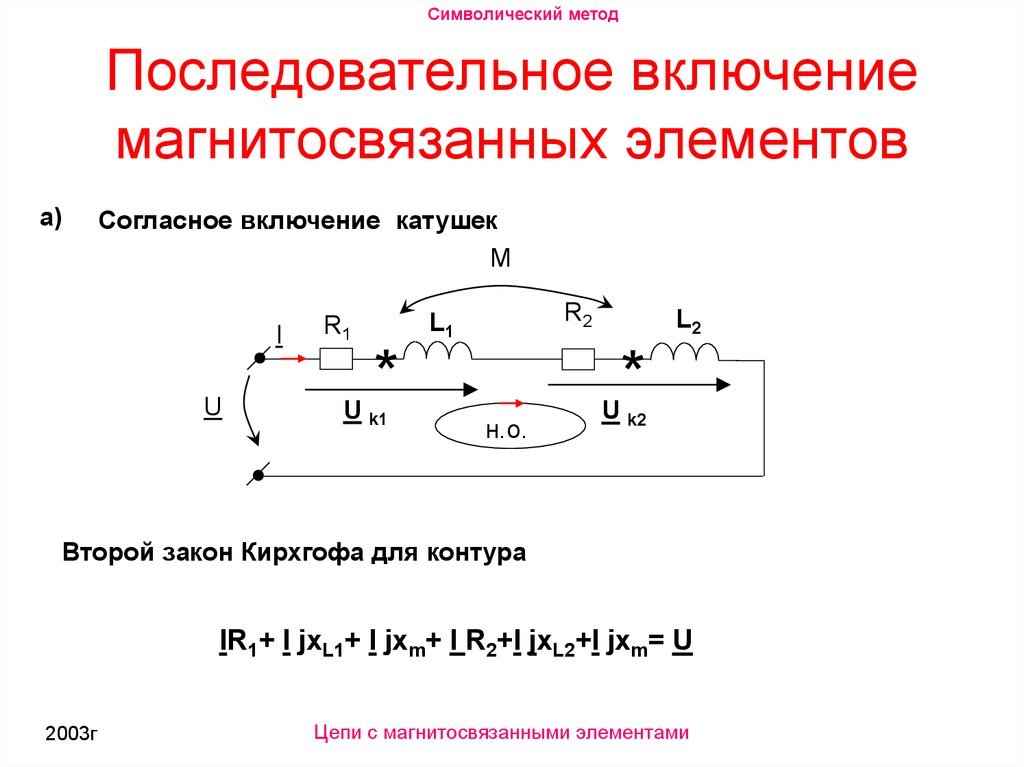




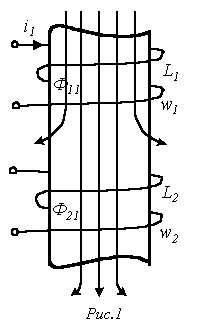
До сих пор при анализе цепей синусоидального тока, содержащих катушки индуктивности, мы учитывали лишь явление самоиндукции, т. Однако в электрических цепях могут возникать потокосцепления взаимной индукции, т. Изменение этих потокосцеплений приводит к возникновению ЭДС взаимной индукции. Цепи, в которых индуцируются ЭДС взаимной индукции, называют индуктивно связанными цепями.


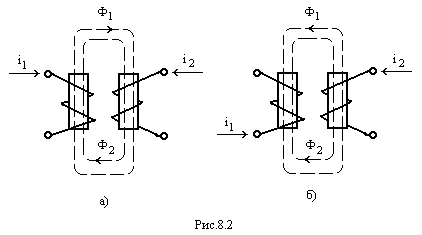


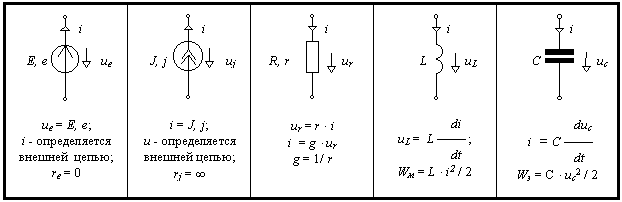


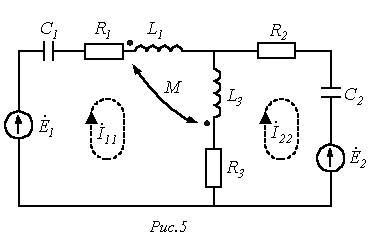

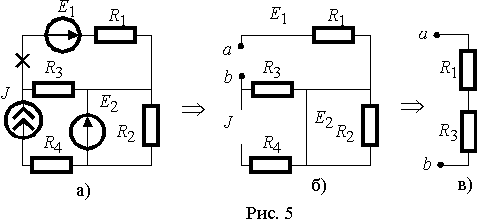
Иногда в литературе можно встретить расчетный метод, который называют развязыванием магнитно-связанных цепей катушек. Метод состоит в том, что исходную схему с магнитно-связанными индуктивностями путем введения дополнительных индуктивностей и изменения имевшихся преобразуют так, что магнитная связь между всеми индуктивностями в преобразованной схеме отсутствует. Так как преобразования осуществляют на основе составленных по законам Кирхгофа уравнений для исходной схемы, то вновь полученная и исходная схемы в расчетном смысле полностью эквивалентны, а расчет схемы после развязывания упрощается за счет возможности применения метода узловых потенциалов.